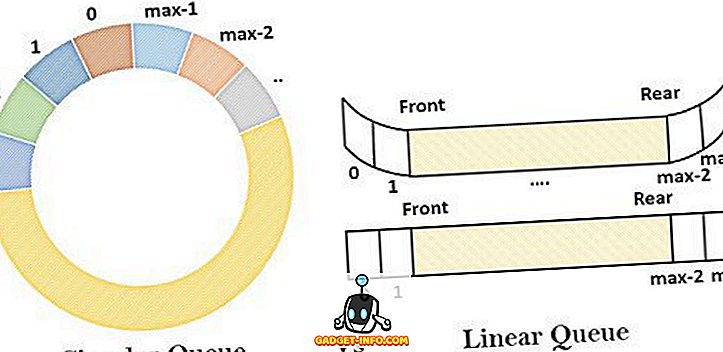
Red se može opisati kao ne-primitivna linearna podatkovna struktura koja slijedi FIFO redoslijed u kojem se elementi podataka ubacuju s jednog kraja (stražnji kraj) i brišu s drugog kraja (prednji kraj). Druge varijacije reda su kružni red, dvostruko završeni red i red prioriteta.
Tablica usporedbe
| Osnova za usporedbu | Linearni red | Kružni red |
|---|---|---|
| Osnovni, temeljni | Organizira elemente podataka i upute u nizu jedan za drugim. | Rasporedi podatke u kružnom uzorku gdje je posljednji element povezan s prvim elementom. |
| Redoslijed izvršenja zadatka | Zadaci se izvršavaju kako bi bili postavljeni prije (FIFO). | Redoslijed izvršavanja zadatka može se promijeniti. |
| Umetanje i brisanje | Novi element se dodaje sa stražnjeg kraja i uklanja s prednje strane. | Umetanje i brisanje se može obaviti na bilo kojem mjestu. |
| Izvođenje | neefikasan | Radi bolje od linearnog reda. |
Definicija linearnog reda čekanja
Linearni red je racionalno prva na prvom popisu naručenih. To je takozvano linearno, jer podsjeća na ravnu liniju gdje su elementi pozicionirani jedan za drugim. Sadrži homogenu zbirku elemenata u koje se dodaju novi elementi na jednom kraju i brišu s drugog kraja. Koncept reda čekanja može se shvatiti na primjeru reda publike koji čeka ispred šaltera za ulaznice da bi dobio kazališnu kartu. U tom redu osoba se pridružuje stražnjem kraju reda kako bi preuzela kartu, a ulaznica se izdaje na prednjem dijelu reda čekanja.
Postoji nekoliko operacija u redu čekanja
- Prvo se red čekanja inicijalizira na nulu (tj. Prazan).
- Odredite je li red prazan ili ne.
- Odredite je li red čekanja pun ili ne.
- Umetanje novog elementa sa stražnjeg kraja (Enqueue).
- Brisanje elementa s prednje strane (Dequeue).
Red se može implementirati na dva načina
- Statički (pomoću polja)
- Dinamično (pomoću pokazivača)
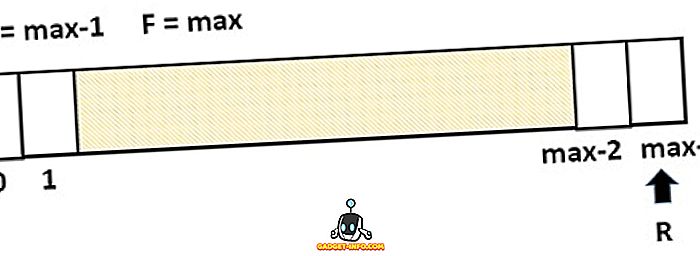
Ograničenje linearnog reda je da stvara scenarij u kojem se novi element ne može dodati u red, čak i ako red sadrži prazna mjesta. Navedena situacija prikazana je na slici dolje. Ovdje stražnji dio pokazuje na posljednji indeks dok su sve kutije još uvijek prazne, ne može se dodati novi element.
Definicija kružnog reda
Kružni red je varijanta linearnog reda koji učinkovito prevladava ograničenje linearnog reda. U kružnom redu novi se element dodaje na prvu poziciju reda ako je zadnja zauzeta, a prostor je dostupan. Kada je riječ o linearnom redu, umetanje se može provesti samo s stražnjeg kraja i brisanja s prednjeg kraja. U punom redu nakon izvođenja niza uzastopnih brisanja u redu za redoslijed pojavljuje se određena situacija u kojoj se novi element ne može dodati, čak ni ako je raspoloživi prostor zato što uvjet podtoka (Rear = max - 1) još uvijek postoji.
Kružni red spaja dva kraja kroz pokazivač gdje prvi element dolazi nakon posljednjeg elementa. Također prati prednje i stražnje dijelove implementirajući neke dodatne logike, tako da može pratiti elemente koje treba umetnuti i izbrisati. Uz to, kružni red ne generira stanje preljeva dok se redak ne popuni u stvarnom stanju.
Neki uvjeti praćeni kružnim redom:
- Front mora pokazivati na prvi element.
- Red će biti prazan ako je Front = Rear.
- Kada se doda novi element, red se povećava za vrijednost jedan (Rear = Rear + 1).
- Kada se element briše iz reda čekanja, prednji dio se povećava za jedan (Front = Front + 1).
Ključne razlike između linearnog reda i kružnog reda
- Linearni red je uređena lista u kojoj su elementi podataka organizirani u redoslijedu koji slijedi. Nasuprot tome, kružni red pohranjuje podatke na kružni način.
- Linearni red slijedi FIFO redoslijed izvršavanja zadatka (element dodan u prvom položaju bit će izbrisan na prvom mjestu). Obrnuto, u kružnom redu redoslijed operacija koje se izvode na elementu može se promijeniti.
- Umetanje i brisanje elemenata je fiksno u linearnom redu tj. Dodavanje od stražnjeg kraja i brisanje s prednjeg kraja. S druge strane, kružni red je sposoban umetnuti i izbrisati element iz bilo koje točke dok se ne zauzme.
- Linearni red troši memorijski prostor, dok kružni red čini učinkovito korištenje prostora.
Implementacija linearnog reda
Algoritam dan dolje ilustrira dodavanje elemenata u red čekanja:
Red treba tri podatkovne varijable uključujući jedan niz za spremanje reda, a drugi za spremanje prednjeg i stražnjeg početnog položaja koji je -1.
insert (item, queue, n, rear) {if (rear == n) a zatim ispiši "queue overflow"; drugo {zadnje = stražnje + 1; red [zadnji] = stavka; }} Algoritam dan dolje ilustrira brisanje elemenata u redu čekanja:
delete_circular (stavka, red, stražnji, prednji) {if (rear == front) zatim ispišite "queue underflow"; inače {front = front + 1; item = queue [front]; }} Implementacija kružnog reda čekanja
Algoritam za tumačenje dodavanja elementa u kružnom redu:
insert_circular (stavka, red, stražnji, prednji) {stražnja = (straga + 1) mod n; ako (ispred == straga) onda ispisati "red je pun"; else {queue [rear] = stavka; }} Algoritam objašnjava brisanje elementa u kružnom redu:
delete_circular (stavka, red čekanja, stražnji, prednji) {if (front == back) zatim print ("queue is empty"); inače {front = front + 1; item = queue [front]; }} Zaključak
Linearni red je neučinkovit u određenim slučajevima gdje su elementi potrebni za prebacivanje na prazna mjesta kako bi se izvršila operacija umetanja. To je razlog zbog kojeg nastaje rasipanje prostora za pohranu, dok kružni red koristi odgovarajuće mjesto za pohranu jer se elementi dodaju na bilo kojem mjestu ako postoji prazan prostor.