
Za razliku od standardne devijacije, to je kvadratni korijen numeričke vrijednosti dobivene izračunavanjem varijance. Mnogi ljudi suprotstavljaju ta dva matematička pojma. Dakle, ovaj članak nastoji rasvijetliti važnu razliku između varijance i standardne devijacije.
Tablica usporedbe
| Osnova za usporedbu | varijacija | Standardno odstupanje |
|---|---|---|
| Značenje | Varijanca je numerička vrijednost koja opisuje varijabilnost opažanja iz svoje aritmetičke sredine. | Standardna devijacija je mjera disperzije opažanja unutar skupa podataka. |
| Što je? | To je prosjek kvadrata odstupanja. | To je srednja kvadratna devijacija. |
| Označeno kao | Sigma-kvadrat (σ ^ 2) | Sigma (σ) |
| Izraženo u | Jedinice kvadrata | Iste jedinice kao i vrijednosti u skupu podataka. |
| Označava | Koliko su udaljeni pojedinci u grupi. | Koliko se opažanja skupa podataka razlikuju od njihove srednje vrijednosti. |
Definicija varijance
U statistici varijance se definira kao mjeru varijabilnosti koja predstavlja koliko su udaljeni članovi grupe. Pronalazi prosječan stupanj u kojem se svako promatranje razlikuje od srednje vrijednosti. Kada je varijanca skupa podataka mala, pokazuje bliskost točaka podataka sa srednjom vrijednošću, dok veća vrijednost varijance predstavlja da su opažanja vrlo raspršena oko aritmetičke sredine i jedan od drugog.
Za nerazvrstane podatke :
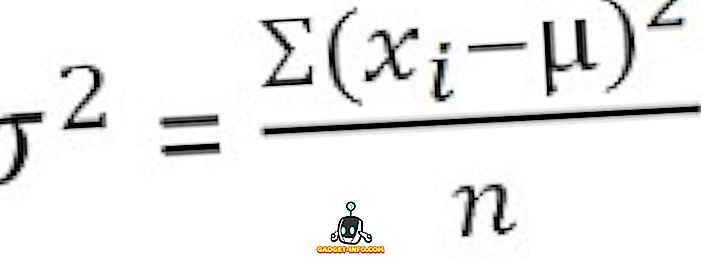
Za grupiranu frekvencijsku distribuciju :
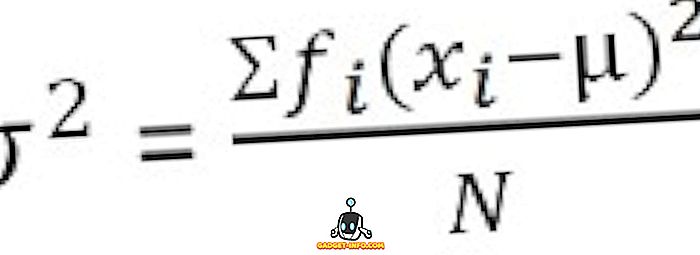
Definicija standardnog odstupanja
Standardna devijacija je mjera koja kvantificira količinu disperzije opažanja u skupu podataka. Niska standardna devijacija je pokazatelj bliskosti rezultata s aritmetičkom sredinom i visokom standardnom devijacijom; rezultati su raspršeni u višem rasponu vrijednosti.
Za nerazvrstane podatke :

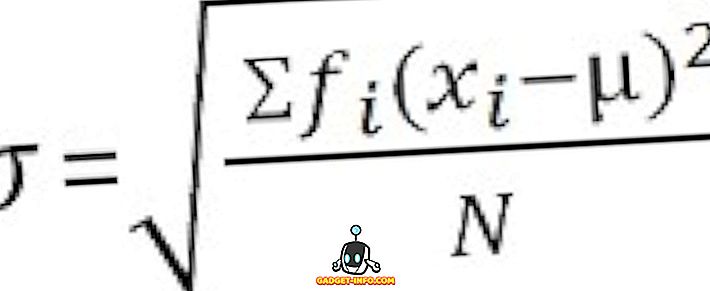
Ključne razlike između varijance i standardnog odstupanja
Razlika između standardne devijacije i varijance može se jasno nacrtati iz sljedećih razloga:
- Varijanca je numerička vrijednost koja opisuje varijabilnost opažanja iz svoje aritmetičke sredine. Standardna devijacija je mjera disperzije opažanja unutar skupa podataka.
- Varijanta nije ništa drugo nego prosjek kvadrata odstupanja. S druge strane, standardna devijacija je srednja kvadratna devijacija.
- Varijanca je označena sigma-kvadratom (σ2), dok je standardna devijacija označena kao sigma (σ).
- Varijanca se izražava u kvadratnim jedinicama koje su obično veće od vrijednosti u danom skupu podataka. Za razliku od standardne devijacije koja je izražena u istim jedinicama kao i vrijednosti u skupu podataka.
- Varijacija mjeri koliko su pojedinci u skupini udaljeni. Suprotno tome, standardno odstupanje mjeri koliko se opažanja skupa podataka razlikuju od njihove srednje vrijednosti.
Ilustracija
Znakovi koje je student postigao u pet predmeta su 60, 75, 46, 58 i 80 respektivno. Morate otkriti standardnu devijaciju i varijance.
Prije svega, morate saznati značenje,

Dakle, prosječne (prosječne) ocjene su 63.8
Sada izračunajte varijancu
| x | (Xa) | (XA) ^ 2 | |
|---|---|---|---|
| 60 | 63.8 | -3, 8 | 14.44 |
| 75 | 63.8 | 11.2 | 125, 44 |
| 46 | 63.8 | -17, 8 | 316, 84 |
| 58 | 63.8 | 5.8 | 33.64 |
| 80 | 63.8 | 16.2 | 262, 44 |
Gdje, X = opažanja
A = aritmetička sredina
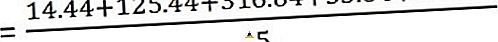
Standardna devijacija je -

sličnosti
- I varijance i standardna devijacija su uvijek pozitivne.
- Ako su sva opažanja u skupu podataka identična, tada će standardna devijacija i varijacija biti nula.
Zaključak
To su osnovni statistički pojmovi, koji igraju ključnu ulogu u različitim sektorima. Standardna devijacija je poželjnija od srednje vrijednosti, budući da je izražena u istim jedinicama kao i one mjerenja, dok je varijacija izražena u jedinicama većim od danog skupa podataka.









